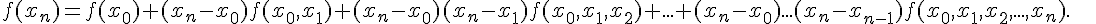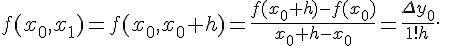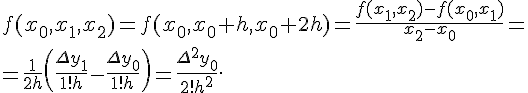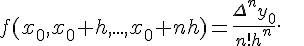- Разностные отношения и их свойства.
- Интерполяционный многочлен Лагранжа.
- Погрешность формулы Лагранжа.
- Пример решения задачи
1 Разностные отношения и их свойства
В том случае, когда значения аргумента являются неравноотстоящими
для исследования и вычисления функции используются разностные
отношения (разделенные разности). Пусть на отрезке ![[a,b] [a,b]](http://virtet.gsu.by/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) заданы произвольные попарно различные узлы интерполирования
заданы произвольные попарно различные узлы интерполирования 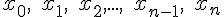 , в
которых известны значения некоторой функции
, в
которых известны значения некоторой функции 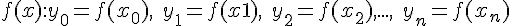 .
.
Разностными отношениями первого порядка называются величины
По разностным отношениям первого порядка составляются разностные отношения второго порядка
Разностные отношения любого порядка 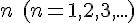 определяются при помощи разностных отношений предыдущего порядка
определяются при помощи разностных отношений предыдущего порядка
 по формуле
по формуле
Используя определение, можно показать, что разностное отношение является симметрической функцией своих аргументов так, что выполняется равенство
Лемма 1 . Если 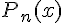 полином степени
полином степени 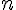 ,
то его конечная разность
,
то его конечная разность 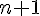 порядка равна нулю для любой
системы попарно различных между собой чисел
порядка равна нулю для любой
системы попарно различных между собой чисел 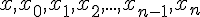
Доказательство. Так как полином 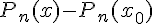 имеет корень в точке
имеет корень в точке 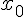 , по определению, получим
, по определению, получим
С учетом (1.24) полином 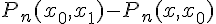 обращается
в нуль в точке
обращается
в нуль в точке 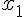 и вторая конечная разность будет полиномом
степени
и вторая конечная разность будет полиномом
степени 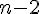
Продолжая аналогичные рассуждения, приходим к выводу, что
и, следовательно, для разностного отношения 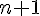 порядка
справедливо равенство (1.28). Лемма доказана.
порядка
справедливо равенство (1.28). Лемма доказана.
Теперь получим выражения разностных отношений всех порядков через значения функции. Из определения разностного отношения первого порядка имеем
Для разностного отношения второго порядка получим
Докажем, что
где 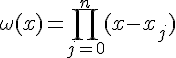 , а
, а 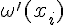 значение производной от
значение производной от 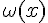 в точке
в точке 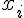 .
.
Доказательство проведем по индукции. Пусть
формула верна для 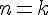 . Тогда
. Тогда
Приведем еще выражение любого значения 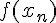 функции через
начальное значение
функции через
начальное значение 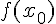 и разностные отношения
и разностные отношения
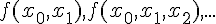 для начальной точки
для начальной точки 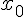 . Из
определения
. Из
определения 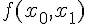 вытекает равенство
вытекает равенство
На основании соотношений (1.32) и (1.30) будем иметь
Используя индукцию, получим
Отметим некоторые свойства разностных отношений
- Свойство аддитивности. Если
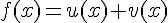 , то
, то
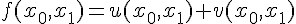 .
.
- Свойство подобия. Если
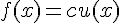 , где
, где 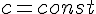 , то
, то
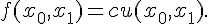
- Свойство симметрии. Разностное отношение
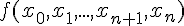 есть симметричная функция своих
агрументов (см. (1.27))
есть симметричная функция своих
агрументов (см. (1.27))
- Если
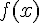 есть многочлен степени
есть многочлен степени 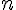 , то разностное
отношение
, то разностное
отношение 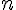 -го порядка
-го порядка 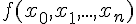 не зависит от
не зависит от
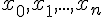 и равняется коэффициенту при старшей степени
и равняется коэффициенту при старшей степени
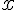 в многочлене
в многочлене 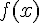 . Все разностные отношения порядка
большего
. Все разностные отношения порядка
большего 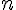 равны нулю (см. лемму 1).
равны нулю (см. лемму 1).
Установим связь между разностными отношениями и конечными
разностями. Предположим, что значения аргумента
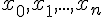 являются равноотстоящими
являются равноотстоящими 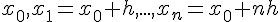 . Тогда получим
. Тогда получим
Для разностного отношения второго порядка имеем

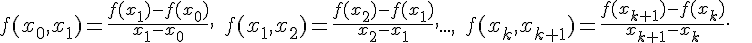
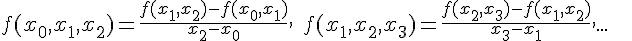
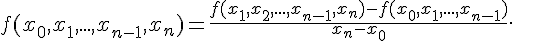
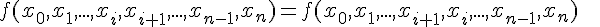
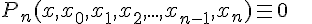
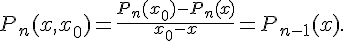
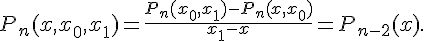
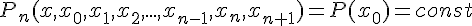
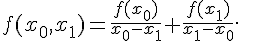
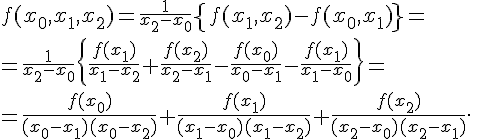
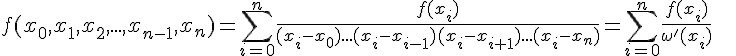
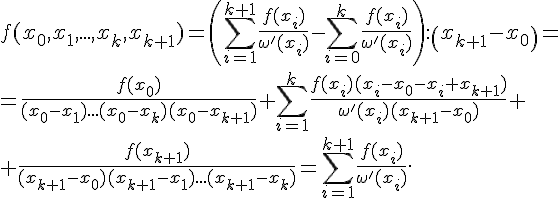
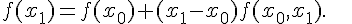
![f(x_2) = f(x_1) + (x_2 - x_1) f(x_1, x_2) = f(x_0) + (x_1 -
x_0)f(x_0,x_1) + \
</p>
<p>
+(x_2 - x_1) \left [ f(x_1,x_2) + (x_2 - x_0) f(x_0,x_1,x_2)
\right ] = \
</p>
<p>
= f(x_0) + (x_2 - x_0) f(x_0,x_1) + (x_2 - x_0)(x_2 - x_1) f(x_0,
x_1, x_2). f(x_2) = f(x_1) + (x_2 - x_1) f(x_1, x_2) = f(x_0) + (x_1 -
x_0)f(x_0,x_1) + \
</p>
<p>
+(x_2 - x_1) \left [ f(x_1,x_2) + (x_2 - x_0) f(x_0,x_1,x_2)
\right ] = \
</p>
<p>
= f(x_0) + (x_2 - x_0) f(x_0,x_1) + (x_2 - x_0)(x_2 - x_1) f(x_0,
x_1, x_2).](http://virtet.gsu.by/filter/tex/pix.php/7adbc1d5359c768151b09c9f4015cd8e.gif)