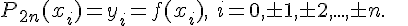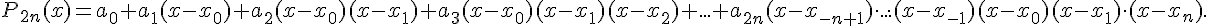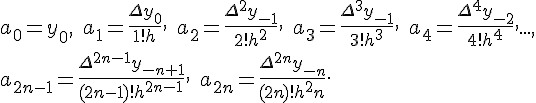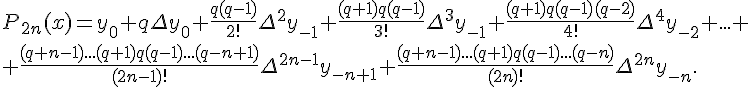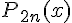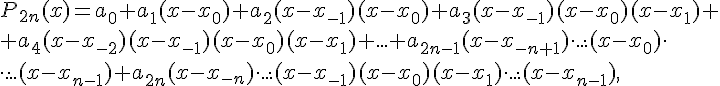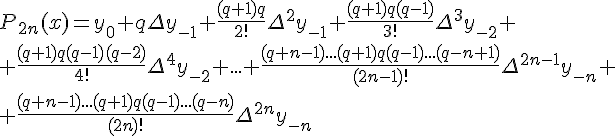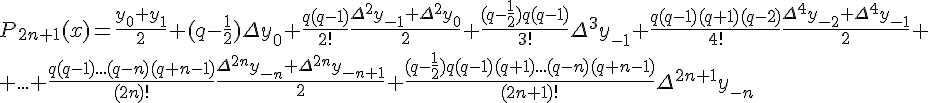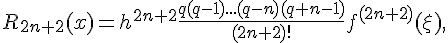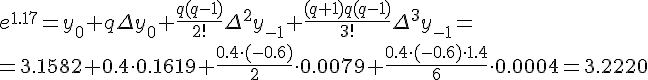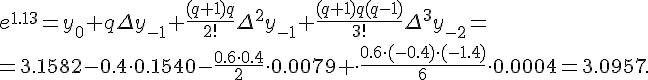- Первая и вторая интерполяционные формулы Гаусса.
- Интерполяционная формула Ньютона-Стирлинга.
- Интерполяционная формула Ньютона-Бесселя.
- Пример решения задач.
1 Первая и вторая интерполяционные формулы Гаусса
Основным недостатком интерполяционных формул Ньютона является то,
что они используют лишь односторонние значения функции. На
практике часто оказывается полезным использовать формулы, в
которых присутствуют как последующие, так и предыдущие значения
функции по отношению к ее начальному значению 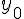 .
.
Рассмотрим 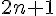 равноотстоящих узлов
равноотстоящих узлов 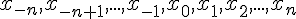 , в которых заданы значения
некоторой функции
, в которых заданы значения
некоторой функции 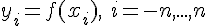 . Требуется
найти полином степени не выше , такой, чтобы выполнялось условие
. Требуется
найти полином степени не выше , такой, чтобы выполнялось условие
Будем искать полином в виде
Поступая по аналогии с выводом первой интерполяционной формулы
Ньютона, для коэффициентов 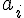 получим следующие выражения
получим следующие выражения
Введем новую переменную 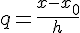 и, подставляя
преобразованные выражения для коэффициентов (1.20) в соотношение
(1.19), получим первую интерполяционную формулу
Гаусса (для интерполирования вперёд)
и, подставляя
преобразованные выражения для коэффициентов (1.20) в соотношение
(1.19), получим первую интерполяционную формулу
Гаусса (для интерполирования вперёд)
Разности 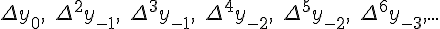 , используемые в этой формуле, образуют
нижнюю ломаную линию в диагональной таблице разностей 1.2. (см.
внизу)
, используемые в этой формуле, образуют
нижнюю ломаную линию в диагональной таблице разностей 1.2. (см.
внизу)
то аналогично (1.21) можно получить вторую интерполяционную формулу Гаусса (для интерполирования назад)
Разности 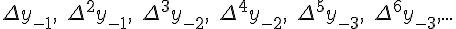 , используемые в этой формуле, образуют
верхнюю ломаную линию в диагональной таблице разностей 1.2.
, используемые в этой формуле, образуют
верхнюю ломаную линию в диагональной таблице разностей 1.2.
Формулы Гаусса применяются для интерполирования в середине
таблицы вблизи 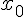 . При этом первая формула Гаусса (1.21)
применяется при
. При этом первая формула Гаусса (1.21)
применяется при 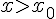 , а вторая (1.22) – при
, а вторая (1.22) – при 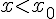 .
.
Таблица 1.2 Диагональная таблица разностей
|
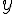
|
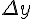
|
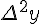
|
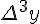
|
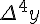
|
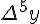
|
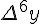
|
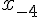
|
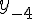
|
||||||
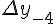
|
|||||||
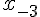
|
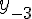
|
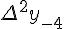
|
|||||
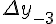
|
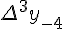
|
||||||
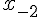
|
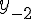
|
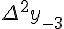
|
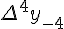
|
||||
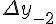
|
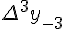
|
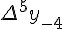
|
|||||
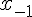
|
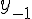
|
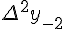
|
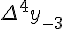
|
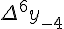
|
|||
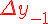
|
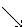
|
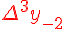
|
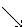
|
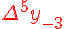
|
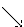
|
||
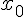
|
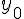
|
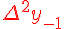
|
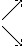
|
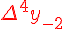
|
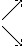
|
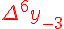
|
|
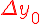
|
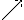
|
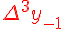
|
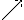
|
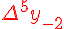
|
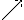
|
||
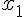
|
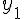
|
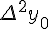
|
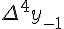
|
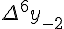
|
|||
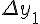
|
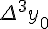
|
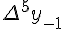
|
|||||

|
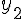
|
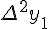
|
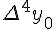
|
||||
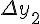
|
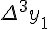
|
||||||
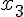
|
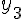
|
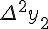
|
|||||
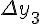
|
|||||||
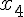
|
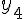
|
2 Интерполяционная формула Ньютона-Стирлинга
Среднее арифметическое первой (1.21) и второй (1.22) формул Гаусса дает интерполяционную формулу Ньютона-Стирлинга
Остаточный член интерполяционной формулы Ньютона-Стирлинга имеет вид
где точка 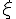 принадлежит отрезку, содержащему узлы
принадлежит отрезку, содержащему узлы 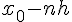 ,
, 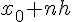 и точку
и точку 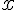 .
.
3 Интерполяционная формула Ньютона-Бесселя
Кроме формулы Ньютона-Стирлинга для 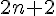 равноотстоящих узлов
равноотстоящих узлов
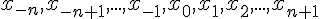 часто
используют интерполяционную формулу
Ньютона-Бесселя, которая имеет вид
часто
используют интерполяционную формулу
Ньютона-Бесселя, которая имеет вид
Остаточный член интерполяционной формулы Ньютона-Бесселя следующий
где точка 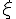 принадлежит отрезку, содержащему узлы
принадлежит отрезку, содержащему узлы 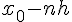 ,
, 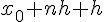 и точку
и точку 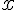 .
.
Формулы с центральными разностями следует использовать, когда
интерполирование проводится в середине таблицы. Если при этом
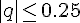 , то целесообразно применять интерполяционную
формулу Ньютона-Стирлинга, а при
, то целесообразно применять интерполяционную
формулу Ньютона-Стирлинга, а при 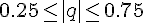 –
интерполяционную формулу Ньютона-Бесселя.
–
интерполяционную формулу Ньютона-Бесселя.
Следует отметить, что все приведенные выше формулы являются
различными формами записи интерполяционного многочлена и поэтому
любая из них может быть использована для интерполирования
функции. Однако с вычислительной точки зрения они не равноценны.
Каждая форма записи организована таким образом, что для
соответствующего случая расположения точки интерполирования
 , в первую очередь вычисляются слагаемые, влияние
которых на результат наиболее существенен.
, в первую очередь вычисляются слагаемые, влияние
которых на результат наиболее существенен.
Замечание. При интерполировании функций,
заданных таблицей с постоянным шагом  аргумента,
рекомендуется руководствоваться следующими правилами:
аргумента,
рекомендуется руководствоваться следующими правилами:
1. Составляя таблицу разностей, определяют максимальный порядок разностей, которые ведут себя правильно. Это означает следующее. Обычно значения функции в таблице приближенные. Если их предельная абсолютная погрешность может достигать половины единицы последнего разряда, то погрешность в разностях первого порядка может достигать уже единицы последнего разряда, в разностях второго порядка – двух единиц последнего разряда и т.д.
Для гладких функций обычно разности убывают с порядком, при некотором порядке становятся почти постоянными, и, следовательно, разности следующего порядка будут малы, но из-за неточности значений функции в дальнейшем с увеличением порядка разности начинают расти, имея беспорядочные знаки. Они-то уже и будут неправильными и их нельзя использовать при интерполировании.
2. Определив наивысший порядок разностей,
которые можно использовать при интерполировании, выбирают
интерполяционную формулу. Если значение  находится близко к
началу отрезка
находится близко к
началу отрезка ![[a,b] [a,b]](http://virtet.gsu.by/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) , то при интерполировании нужно
использовать формулу Ньютона для интерполирования вперед, а при
, то при интерполировании нужно
использовать формулу Ньютона для интерполирования вперед, а при
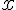 близких к концу отрезка – формулу Ньютона для
интерполирования назад, так как только эти формулы допускают
использование правильных разностей до максимального порядка. Если
же значения
близких к концу отрезка – формулу Ньютона для
интерполирования назад, так как только эти формулы допускают
использование правильных разностей до максимального порядка. Если
же значения 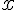 , для которого нужно вычислить значение функции,
находится на отрезке
, для которого нужно вычислить значение функции,
находится на отрезке ![\left [ x_i, x_{i+1} \right ] \left [ x_i, x_{i+1} \right ]](http://virtet.gsu.by/filter/tex/pix.php/b44884086a31e2a248b3407ac79ca14b.gif) , то нужно
применять формулы Стирлинга или Бесселя, применяя за начальный
узел в них узел
, то нужно
применять формулы Стирлинга или Бесселя, применяя за начальный
узел в них узел 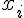 или
или 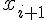 в зависимости от того,
который из них ближе к
в зависимости от того,
который из них ближе к 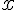 . При этом применяется формула
Стирлинга, если
. При этом применяется формула
Стирлинга, если 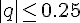 и формула Бесселя при
и формула Бесселя при 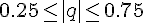 . Кроме того, при использовании формулы Стирлинга
необходимо учитывать последнюю правильную разность нечетного
порядка, а при использовании формулы Бесселя – последнюю
правильную разность четного порядка.
. Кроме того, при использовании формулы Стирлинга
необходимо учитывать последнюю правильную разность нечетного
порядка, а при использовании формулы Бесселя – последнюю
правильную разность четного порядка.
4 Пример решения задач
Для функции 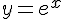 построить таблицу значений функции на
отрезке
построить таблицу значений функции на
отрезке ![[1.15;1.30], \quad h = 0.05 [1.15;1.30], \quad h = 0.05](http://virtet.gsu.by/filter/tex/pix.php/54d9457b9ae3bd4f445f27091d07b247.gif) . С помощью
интерполяционной формулы Гаусса найти значение функции
. С помощью
интерполяционной формулы Гаусса найти значение функции
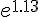 и
и 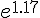 .
.
Решение.
Составляем таблицу разностей
|
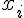
|
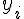
|
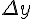
|
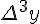
|
|
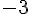
|
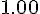
|

|
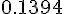
|
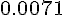
|
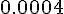
|
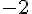
|
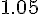
|
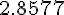
|
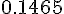
|
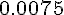
|
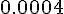
|
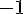
|
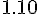
|
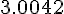
|
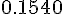
|
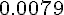
|
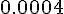
|
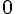
|
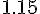
|
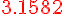
|
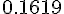
|
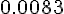
|
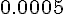
|
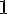
|
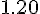
|
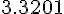
|
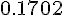
|
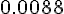
|
|
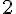
|
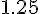
|
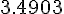
|
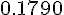
|
||
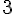
|
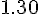
|
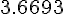
|
Замечаем, что третьи разности практически постоянны. Поэтому в
формулах (1.21) и (1.22) достаточно взять 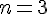 .
.
Для вычисления 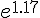 используем формулу (1.21) (поскольку
1.17>1.15) при
используем формулу (1.21) (поскольку
1.17>1.15) при 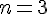 и
и 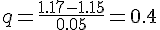 :
:
Значение 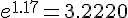 расположено между
расположено между
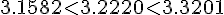 (см. таблицу, т.к.
(см. таблицу, т.к.
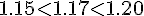 ), следовательно, значение функции в
точке нашли правильно.
), следовательно, значение функции в
точке нашли правильно.
Для вычисления 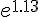 используем формулу (1.22)
(поскольку
используем формулу (1.22)
(поскольку  ) при
) при 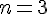 и
и 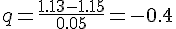 :
: