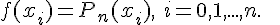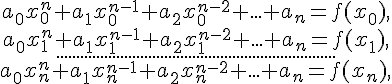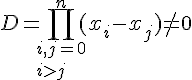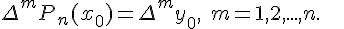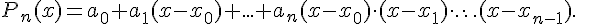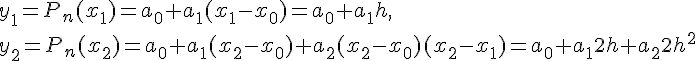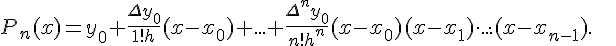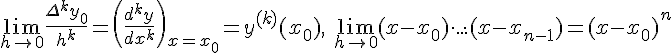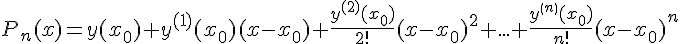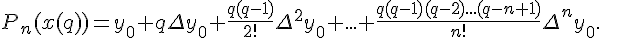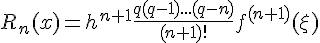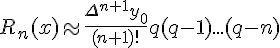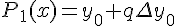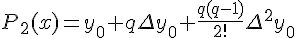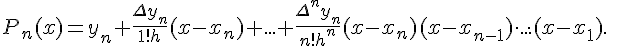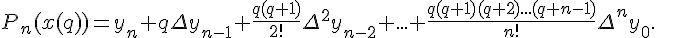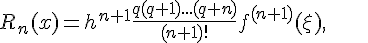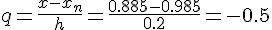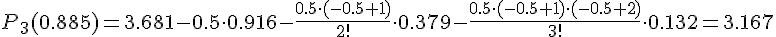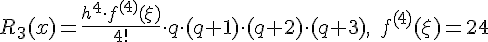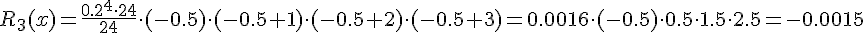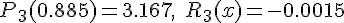- Теорема о существовании интерполяционного многочлена.
- Первая интерполяционная формула Ньютона.
- Вторая интерполяционная формула Ньютона.
- Примеры решения задач
1 Теорема о существовании интерполяционного многочлена
Пусть на отрезке ![[a,b] [a,b]](http://virtet.gsu.by/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) в
в 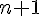 узле
узле 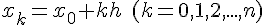 заданы значения ограниченной функции
заданы значения ограниченной функции
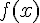 :
: 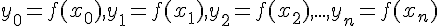 . Поставим задачу нахождения полинома
. Поставим задачу нахождения полинома 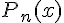 степени не
степени не 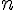 выше такого, чтобы выполнялось условие
выше такого, чтобы выполнялось условие
Теорема 1. Существует и притом единственный
многочлен степени не выше 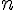 , для которого выполняется условие
(1.10).
, для которого выполняется условие
(1.10).
Доказательство. Пусть многочлен 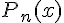 имеет
вид (1.3). Используя (1.10) для определения коэффициентов
имеет
вид (1.3). Используя (1.10) для определения коэффициентов
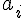 , получим систему (1.4) линейных алгебраических уравнений,
которую запишем в виде
, получим систему (1.4) линейных алгебраических уравнений,
которую запишем в виде
Определитель системы (1.11) является определителем Вандермонда и имеет вид
Следовательно, для системы различных между собой узлов система (1.11) имеет единственное решение. Теорема доказана.
2 Первая интерполяционная формула Ньютона
Очевидно, что условие (1.10) эквивалентно условию
Будем искать интерполяционный полином в виде
Значения коэффициентов 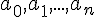 находим из условия
совпадения значений исходной функции и многочлена в узлах.
Полагая
находим из условия
совпадения значений исходной функции и многочлена в узлах.
Полагая 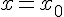 из (1.13) найдем
из (1.13) найдем 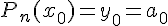 .
Далее, последовательно придавая
.
Далее, последовательно придавая 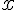 значения
значения 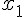 и
и 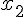 получаем,
получаем,
Откуда, применяя (1.12), для коэффициента 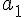 получим
выражение
получим
выражение 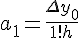 , а для
, а для 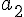 -
-
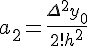 .(из учебника "Численные
методы на базе Mathcad")
.(из учебника "Численные
методы на базе Mathcad")
Продолжая наши рассуждения, запишем формулу для любого 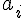 :
:
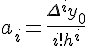 . Подставляя в (1.13)
выражения для коэффициентов
. Подставляя в (1.13)
выражения для коэффициентов 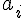 через конечные разности,
получим первую интерполяционную формулу Ньютона
через конечные разности,
получим первую интерполяционную формулу Ньютона
При 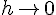 справедливы следующие пределы
справедливы следующие пределы
Отсюда следует, что при 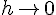 интерполяционный
полином (1.14) принимает вид полинома Тейлора
интерполяционный
полином (1.14) принимает вид полинома Тейлора
Для практический целей формулу Ньютона (1.14) удобнее записывать
в несколько ином виде. Введем переменную 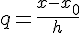 . Тогда
. Тогда 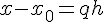 . Таким образом, для полинома
. Таким образом, для полинома 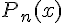 получим выражение
получим выражение
Формулу (1.15) выгодно использовать для интерполирования в
окрестности начального значения 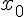 . Поэтому ее часто
называют формулой для интерполирования вперед. В
этой формуле из таблицы конечных разностей используются
. Поэтому ее часто
называют формулой для интерполирования вперед. В
этой формуле из таблицы конечных разностей используются
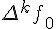 верхней диагонали.
верхней диагонали.
Остаточный член в формуле (1.15) имеет вид
где 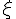 – некоторая внутренняя точка наименьшего промежутка,
содержащего все узлы
– некоторая внутренняя точка наименьшего промежутка,
содержащего все узлы 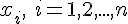 и точку
и точку 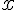 . При
наличии дополнительного узла
. При
наличии дополнительного узла 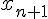 на практике пользуются
более удобной приближенной формулой
на практике пользуются
более удобной приближенной формулой
При 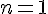 из (1.15) получается формула линейного
интерполирования
из (1.15) получается формула линейного
интерполирования
При 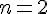 из (1.15) имеет место формула
параболического или квадратического интерполирования
из (1.15) имеет место формула
параболического или квадратического интерполирования
3 Вторая интерполяционная формула Ньютона
Первая интерполяционная формула Ньютона практически неудобна для
интерполирования функций в конце таблицы. Поэтому когда точка
интерполирования лежит вблизи точки 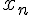 удобно пользоваться
второй интерполяционной формулой Ньютона,
которая имеет вид
удобно пользоваться
второй интерполяционной формулой Ньютона,
которая имеет вид
Вводя новую переменную 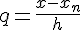 , эту формулу
перепишем в виде
, эту формулу
перепишем в виде
В формуле (1.17) из таблицы конечных разностей используются 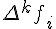 нижней диагонали.
нижней диагонали.
Остаточный член формулы (1.17) имеет вид
где точка 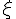 имеет тот же смысл, что и ранее.
имеет тот же смысл, что и ранее.
Отметим, что формулы Ньютона используются и для экстраполирования
функций. Если 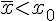 , то для
экстраполирования назад используют первую интерполяционную
формулу Ньютона. Если
, то для
экстраполирования назад используют первую интерполяционную
формулу Ньютона. Если 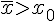 , то для
экстраполирования вперед используют вторую интерполяционную
формулу Ньютона. Следует заметить, что операция
экстраполирования менее точна, чем операция интерполирования в
узком смысле.
, то для
экстраполирования вперед используют вторую интерполяционную
формулу Ньютона. Следует заметить, что операция
экстраполирования менее точна, чем операция интерполирования в
узком смысле.
4 Примеры решения задач
Используя первую или вторую интерполяционную формулу Ньютона для
равноотстоящих узлов интерполяции вычислить значение функции,
заданной таблично в точке 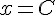 . Оценить погрешность
интерполяционной формулы.
. Оценить погрешность
интерполяционной формулы.
Построить таблицу данных из условия 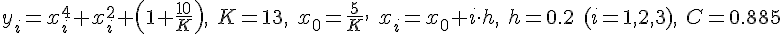 .
.
Решение.
Поскольку точка 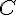 лежит ближе к концу отрезка
интерполирования и узлы
лежит ближе к концу отрезка
интерполирования и узлы 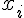 – равноотстоящие, поэтому
применяем вторую формулу Ньютона для равноотстоящих узлов (1.17)
и учитываем, что
– равноотстоящие, поэтому
применяем вторую формулу Ньютона для равноотстоящих узлов (1.17)
и учитываем, что 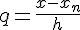 .
.
Составляем таблицу конечных разностей :
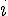
|
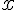
|
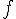
|
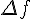
|
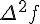
|
|
| 0 | 0.385 | 1.93943 | 0.28915 | 0.24747 | 0.13152 |
| 1 | 0.585 | 2.22857 | 0.53662 | 0.37899 | |
| 2 | 0.785 | 2.76519 | 0.9156 | ||
| 3 | 0.985 | 3.68079 |
Подставляем в формулу
Сделаем проверку по таблице: 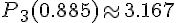 (действительно, это значение расположено между
(действительно, это значение расположено между 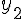 и
и 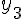 см. таблицу).
см. таблицу).
Оценим погрешность , используя формулу (1.17`)