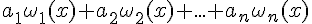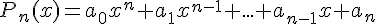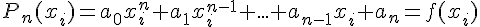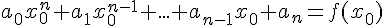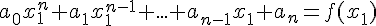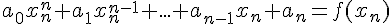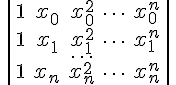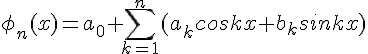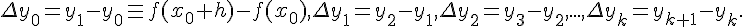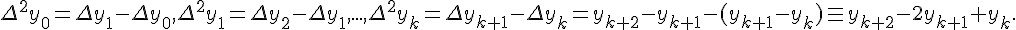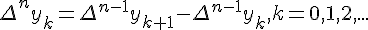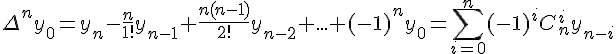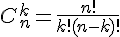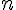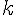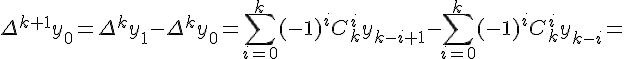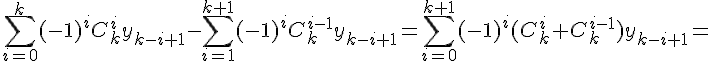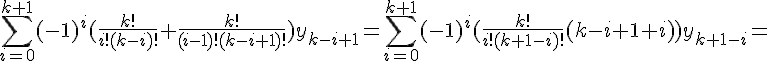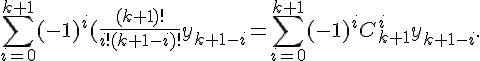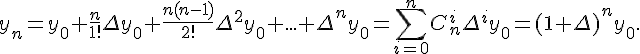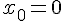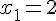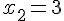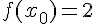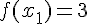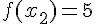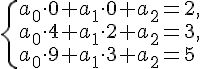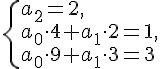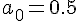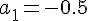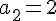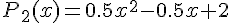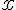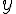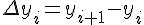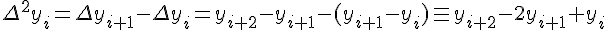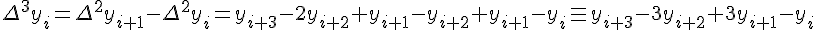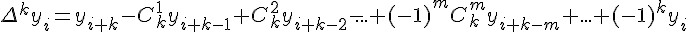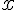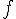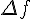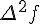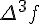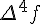- Постановка задачи интерполирования.
- Примеры интерполяционных функций.
- Конечные разности и их свойства.
- Примеры решения задач.
1 Постановка задачи интерполирования
Рассмотрим на отрезке
![[a,b] [a,b]](http://virtet.gsu.by/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) некоторую m – кратно
дифференцируемую функцию
некоторую m – кратно
дифференцируемую функцию 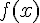 . Пусть в
. Пусть в 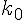 точках
точках
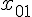 ,
, 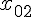 , ... ,
, ... , 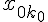 известны ее значения
известны ее значения
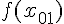 ,
, 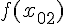 , ...,
, ..., 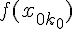 в
в 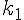 точках
точках 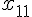 ,
, 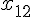 , ...,
, ..., 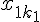 известны значения
первой производной
известны значения
первой производной 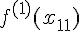 ,
, 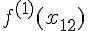 , ...,
, ...,
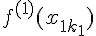 и в
и в 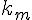 точках известны значения m
–ой производной
точках известны значения m
–ой производной 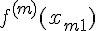 ,
, 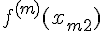 , ...,
, ...,
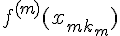 .
.Значения функции и ее производных называются данными интерполирования, а точки
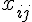 – узлами
интерполирования.
– узлами
интерполирования.Задача интерполирования заключается в отыскании функции
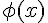 из некоторого класса
из некоторого класса 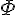 такой, что
выполняется условие
такой, что
выполняется условие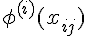 =
= 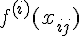 ,
, 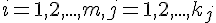 (1.1)
(1.1)Пусть
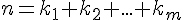 . Рассмотрим на отрезке
. Рассмотрим на отрезке
![[a,b] [a,b]](http://virtet.gsu.by/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) последовательность линейно независимых m – кратно
дифференцируемых функций:
последовательность линейно независимых m – кратно
дифференцируемых функций: 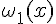 ,
, 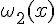 , ...,
, ...,
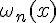 . В качестве семейства
. В качестве семейства  возьмем всевозможные
линейные комбинации первых n функций с произвольными
коэффициентами
возьмем всевозможные
линейные комбинации первых n функций с произвольными
коэффициентами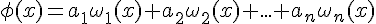 .
.
Из условия (1.1) получим систему линейных
алгебраических уравнений для определения коэффициентов 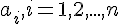
Система (1.2) будет иметь единственное решение в том случае, если ее определитель отличен от нуля.
2 Примеры интерполяционных функций
Приведем примеры интерполяционных функций.
1. Рассмотрим следующую систему линейно независимых функций: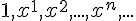 .
.
Тогда семейством 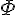 является совокупность алгебраических
многочленов вида
является совокупность алгебраических
многочленов вида
Геометрически это означает, что нужно найти алгебраическую кривую
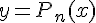 , проходящую через систему точек
, проходящую через систему точек 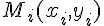
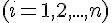 , (Рис. 1.1).
, (Рис. 1.1).

Рис.1.1 Интерполяционный многочлен
Система уравнений, из которой определяютсякоэффициенты 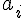 из
(1.3),будет
из
(1.3),будет
или
.......................................................................
Ее определитель является определителем
Вандермонда,
и он отличен от нуля для различных между собой значениях 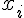 .
.
Интерполирование полиномами вида (1.3) называется
алгебраическим. Многочлен 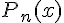 называется
интерполяционным многочленом. Точки
называется
интерполяционным многочленом. Точки 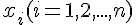 называются узлами интерполяции.
называются узлами интерполяции.
2. Для интерполирования периодических функций с периодом 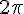 применяется система тригонометрических функций:
применяется система тригонометрических функций: 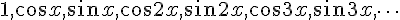 . Линейная
комбинация первых
. Линейная
комбинация первых 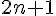 функций является тригонометрическим
многочленом степени
функций является тригонометрическим
многочленом степени 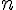
Интерполирование с помощью полиномов (1.5) называется тригонометрическим.
Пусть для функции 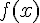 построена интерполирующая функция
построена интерполирующая функция
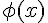 . Тогда, если определяется значение
. Тогда, если определяется значение 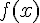 в точке
в точке
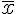 , лежащей внутри отрезка интерполирования
, лежащей внутри отрезка интерполирования
![[a,b] [a,b]](http://virtet.gsu.by/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) , то такое восстановление функции называется
интерполяцией. Если же точка
, то такое восстановление функции называется
интерполяцией. Если же точка 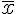 лежит вне отрезка
лежит вне отрезка ![[a,b] [a,b]](http://virtet.gsu.by/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.gif) , то такое восстановление функции
называется экстраполяцией.
, то такое восстановление функции
называется экстраполяцией.
3 Конечные разности и их свойства
Конечные разности в вычислительной математике имеют значение, аналогичное дифференциалам в анализе бесконечно малых величин.
Пусть даны равноотстоящие друг от друга узлы 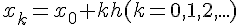 и известны соответствующие
значения функции
и известны соответствующие
значения функции 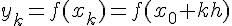 . Здесь
. Здесь 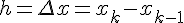 – некоторое фиксированное значение
аргумента. (или рассмотрим таблицу значений функции с
постоянным шагом
– некоторое фиксированное значение
аргумента. (или рассмотрим таблицу значений функции с
постоянным шагом 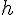 , для которой значения
аргумента определяются формулой
, для которой значения
аргумента определяются формулой 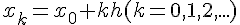 , значения функции
, значения функции 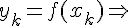 узлы
узлы 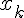 – равноотстоящие).
– равноотстоящие).
Конечными разностями нулевого порядка
называются величины 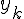 равные значениям функции
равные значениям функции 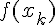 в узлах
в узлах 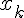 , т.е.
, т.е. 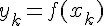 . Конечной разностью
первого порядка называется разность между значениями
функции в соседних узлах интерполяции
. Конечной разностью
первого порядка называется разность между значениями
функции в соседних узлах интерполяции
Конечные разности второго порядка определяются равенствами по отношению к разностям первого порядка (дельта два игрек нулевое)
Разности n -го порядка определяются по формуле
Конечные разности любого порядка легко выражаются через значения функции
Доказательство проведем по индукции. Пусть эта
формула верна для 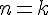 . Покажем, что она будет верна и при
. Покажем, что она будет верна и при
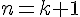 .
.
Аналогично доказывается формула
Из определения конечных разностей вытекают следующие свойства
- если
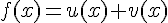 , то
, то 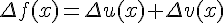 ; если функция представлена в виде суммы
двух функций, то конечная разность исходной функции
представляется как сумма конечных разностей слагаемых.
; если функция представлена в виде суммы
двух функций, то конечная разность исходной функции
представляется как сумма конечных разностей слагаемых.
- если
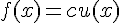 ,
, 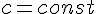 , то
, то 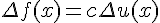 ; при умножении функции на
; при умножении функции на 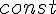 , конечные
разности умножаются на тот же множитель.
, конечные
разности умножаются на тот же множитель.
- конечные разности
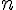 –го порядка от многочлена степени
–го порядка от многочлена степени 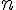 постоянны
постоянны 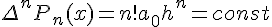 , а
, а 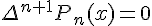 ;
;
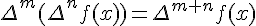 .
.
Таблицу конечных разностей обычно располагают следующим образом:
Таблица 1.1 Конечные разности
|
|
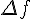
|
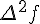
|
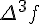
|
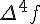
|
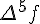
|
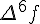
|
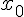
|
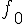
|
||||||
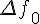
|
|||||||
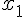
|
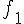
|
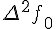
|
|||||
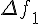
|
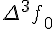
|
||||||
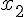
|
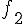
|
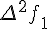
|
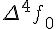
|
||||
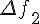
|
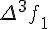
|
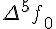
|
|||||
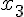
|
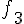
|
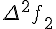
|
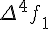
|
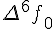
|
|||
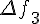
|
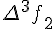
|
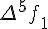
|
|||||
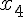
|
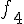
|
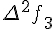
|
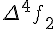
|
||||
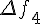
|
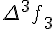
|
||||||
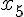
|
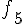
|
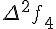
|
|||||
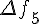
|
|||||||
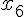
|
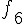
|
4 Примеры решения задач.
1. Заданы значения
Построим многочлен вида (1.3) второй степени 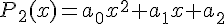 , для которого
, для которого 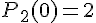 ,
, 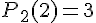 ,
,
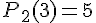 .
.
Решение.
Составим систему (1.4)
Не трудно проверить, что 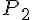 удовлетворяет поставленным
условиям.
удовлетворяет поставленным
условиям.
2. Составим таблицу значений функции 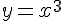 с шагом
с шагом 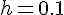 на отрезке
на отрезке ![[0.0;0.5] [0.0;0.5]](http://virtet.gsu.by/filter/tex/pix.php/50a7084a5bce332eeb50ed9be98e5535.gif) и найдем
конечные разности различных порядков.
и найдем
конечные разности различных порядков.
Решение.
Значения функции и конечные разности запишем в таблицу вида 1.1
|
0.0 |
0.000 |
|||||
|
0.001 |
||||||
|
0.1 |
0.001 |
0.006 |
||||
|
0.007 |
0.006 |
|||||
|
0.2 |
0.008 |
0.012 |
0 |
|||
|
0.019 |
0.006 |
0 |
||||
|
0.3 |
0.027 |
0.018 |
0 |
|||
|
0.037 |
0.006 |
|||||
|
0.4 |
0.064 |
0.24 |
||||
|
0.061 |
||||||
|
0.5 |
0.125 |
3. Задана таблица значений функции
|
2 |
4 |
6 |
8 |
10 |
|
|
0.03 |
0.11 |
0.27 |
0.50 |
0.83 |
Найдем конечные разности.
Решение.
Значения функции и конечные разности будем записывать в таблицу вида 1.1.
Выразим конечные разности высших порядков через значения функции, заданные в узлах интерполяции.
Вторая конечная разность
Третья конечная разность
|
2 |
0.3 |
||||
|
0.08 |
|||||
|
4 |
0.11 |
0.08 |
|||
|
0.16 |
-0.01 |
||||
|
6 |
0.27 |
0.07 |
0.04 |
||
|
0.23 |
0.03 |
||||
|
8 |
0.50 |
0.10 |
|||
|
0.33 |
|||||
|
10 |
0.83 |